Кохерентната амплитуда на един прозорец a(k) с дължина N е
$$CG=\frac{1}{N} \sum_{k=0}^{N-1} a(k)$$
Както е изчислена, тази кохерентна амплитуда е нормализирана за дължината на прозореца N.
Пример на приложението на кохерентната амплитуда
Вземи един сигнал x(k) с честота 60 Hz върху пробната честота 400 Hz.
$$x(k)=\sin(\frac{2\pi k \,60}{400})$$
Да предположим, че използваме дискретизираното преобразуване на Фурие с 20 компонента за да изчислим амплитудата |H(m)| на честотите 0 Hz, 20 Hz,…, 380 Hz в този сигнал.
$$H(m)=\sum_{k=0}^{M-1} x(k) e^{-\frac{2\pi\,j\,k\,m}{N}}$$ $$=\sum_{k=0}^{M-1} x(k) \cos(\frac{2\pi\,k\,m}{N})-j \sum_{k=0}^{M-1} x(k) \sin(\frac{2\pi\,k\,m}{N})$$ $$|H(m)|=\sqrt{(Re(H(m)))^2+(Im(H(m)))^2}$$
M = 20, m = 0, 1, …, M – 1. Амплитудата на 60 Hz в x(k) ще бъде изчислена като 10, а амплитудите на останалите честоти ще бъде приблизително нула. Това е така, защото честотата 60 Hz е кратно на стъпката на преобразуването на Фурие, равна на 20 Hz, и се хваща добре в първите 20 проби. Изчисленото амплитудно съдържание на x(k) е показано в следната графика.
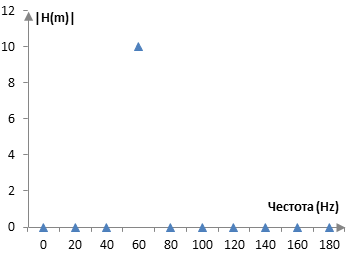
Преобразуването на Фурие не е толкова прецизно при всички честоти. При x(k) = 55 Hz например ще получим следната графика.
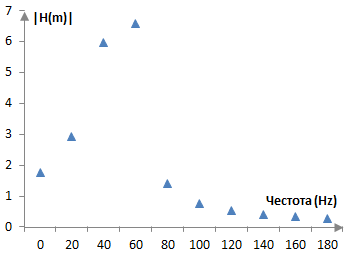
Този сигнал не се хваща добре (не извършва едно цяло число цикли) в първите 20 проби и затова неговата амплитуда се разлива върху останалите компоненти на преобразуването на Фурие. Това е спектрално разсейване.
За да облекчим това спектрално разсейване, можем да използваме един прозорец върху сигнала x(k). Следната графика показва амплитудното съдържание на сигнала, изчислено с преобразуването на Фурие, преди и след прилагането на прозореца на Хан върху сигнала. Прозорецът на Хан, който се използва тук, е с дължина M = 20, дължината на преобразуването на Фурие. Тази графика е изчислена с нагаждане за кохерентната амплитуда на прозореца, както е обяснено по-долу.
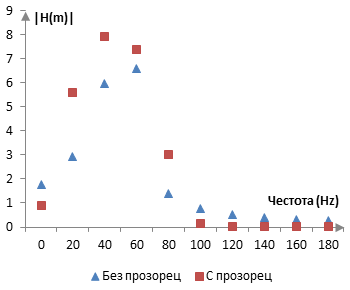
Прозорецът намалява спектралното разсейване, защото намалява сигнала в двата края на 20-те семпли и, следователно, дали сигнала се хваща добре в тези 20 семпли или не, не е толкова важно. В горната графика, амплитудите с прозореца са по-концентрирани около действителната честота на сигнала. Преобразуването на Фурие е по-прецизно.
Следното е сигнала преди и след прозореца.
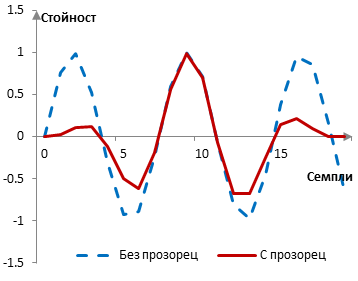
Когато прозорецът е приложен към сигнала обаче, амплитудите на сигнала, които ще бъдат изчислени с преобразуването на Фурие, ще намалят. Кохерентната амплитуда на прозореца измерва това намаление. Амплитудите, изчислени с преобразуването на Фурие, трябва да се настроят (разделят) с кохерентната амплитуда за да са сравними. Кохерентната амплитуда на прозореца на Хан от 20 точки в този пример е 0.475. При прозорци с по-голяма дължина, кохерентната амплитуда ще клони към 0.5.
Подобно "спектрално разсейване " се получава и когато дискретното преобразуване на Фурие е изчислено за точки между самите компоненти на преобразуването. Вземи следната графика.
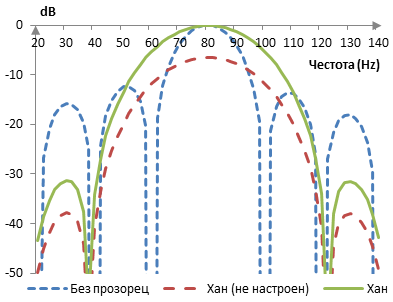
Изчисления, които са подобни на тези на дискретното преобразуване на Фурие, се използват за да се анализира честотното съдържание на една проста вълна с 80 Hz със и без прозореца на Хан. Прозорецът на Хан намалява спектралното разсейване, но резултатът от прозореца на Хан трябва да се настрои със кохерентната амплитуда за да даде очакваната амплитуда от 0 dB при 80 Hz.
Кохерентни амплитуди на често срещани прозорци
Следното са кохерентните амплитуди на често срещани прозорци (с определенията за прозорците в този сайт).
| Бартлет и Хан | 0.50 |
| Блекмън Точен Блекмън Обобщен Блекмън α = 0.05 α = 0.20 α = 0.35 |
0.42 0.43 0.47 |
| Блекмън и Харис | 0.36 |
| Блекмън и Нътол | 0.36 |
| Боумън | 0.40 |
| Долф и Чебишев ω0 = 0.1 ω0 = 0.2 ω0 = 0.3 |
0.34 0.25 0.20 |
| Плосък | 0.22 |
| Гаус σ = 0.3 σ = 0.5 σ = 0.7 Приблизителен ограничен на Гаус σ = 0.3 σ = 0.5 σ = 0.7 Обобщен нормален α = 2 α = 4 α = 6 |
0.37 0.60 0.74 0.37 0.60 |
| Хеминг | 0.54 |
| Хан | 0.50 |
| Хан и Поасон α = 0.3 α = 0.5 α = 0.7 |
0.46 0.43 0.41 |
| Кайзер α = 0.5 α = 1.0 α = 5.0 |
0.85 0.67 0.42 |
| Кайзер и Бесел | 0.40 |
| Ланцош | 0.59 |
| Нътол | 0.36 |
| Парзън | 0.69 |
| Клин на Планк ε = 0.2 ε = 0.4 ε = 0.5 |
0.80 0.60 0.50 |
| Поасон α = 0.2 α = 0.5 α = 0.8 |
0.91 0.79 0.69 |
| Степен на косинуса α = 1.0 α = 2.0 α = 3.0 |
0.64 0.50 0.42 |
| Правоъгълен | 1.00 |
| Синусоиден | 0.64 |
| Триъгълен | 0.50 |
| Тъки α = 0.3 α = 0.5 α = 0.7 |
0.65 0.75 0.85 |
| Ултрасферичен (x0 = 1) μ = 2 μ = 3 μ = 4 |
0.68 0.55 0.48 |
| Уелч | 0.67 |
Добави нов коментар