Преобразуване с вълнички на Хаар

Определението на преобразуването с вълнички на Хаар е по-долу. Има много начини, по които преобразуването може да се изпише. Определението тук е изведено от следния пример за разлагането на един кратък аудио сигнал.

Пример на преобразуване с вълнички на Хаар от осмо ниво на един сигнал

Вземи следния примерен сигнал.

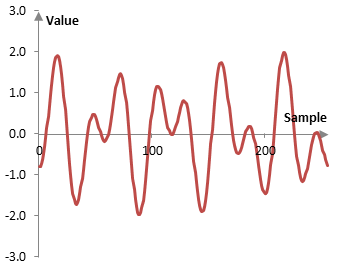
Този примерен сигнал е сумата на две прости синусоиди, една от които е с честота 5 Hz и фаза равна на нула (т.e., вълната започва със стойност нула при проба нула) и другата от които е с честота 9 Hz и е изместена надясно с 10 проби. Пробната честота е 256 Hz и графиката по-горе показва 256 проби (1 секунда) от сигнала.

Нека стойността на този сигнал при проба k е x(k). Нека K = 256 и, за 1 секунда, k = 0, 1, …, K – 1. Изчисли

$$a_1(j)=\frac{x(k-1)+x(k)}{\sqrt{2}}$$ $$b_1(j)=\frac{x(k-1)-x(k)}{\sqrt{2}}$$

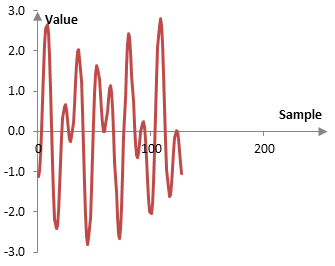
за j = 0, 1, …, K/2 и k = 2j + 1. Изчисленият сигнал a₁(j) е едно средно аритметично на x(k). Изглажда сигнала x(k) и премахва част от променливостта между всеки две съседни проби. Също така и компресира сигнала x(k) във времето. Сигнала b₁(j) съдържа колебанията, които сигнала a₁(j) премахва. Следното е графиката на a_1(j).

Забележи следното:

• x(k) може да бъде възстановен от сигналите a₁(j) и b₁(j)

$$x(k-1)=\frac{a_1(j)+b_1(j)}{\sqrt{2}}$$ $$x(k)=\frac{a_1(j)-b_1(j)}{\sqrt{2}}$$

• a₁(j) и b₁(j) запазват енергията на сигнала x(k) (с изключение на потенциални проблеми свързани с квантуването; виж Дитеринг), в смисъл, че

$$a_1(j)^2+b_1(j)^2=x(k-1)^2+x(k)^2$$

• Често, много от стойностите на b₁(j) са сравнително малки. Този факт се използва по-долу. По принцип, според теоремата за дискретизацията, един сигнал дискретизиран с пробната честота fs може да представи честотите между 0 и fs/2. Колебанията ще са големи само ако сигнала съдържа високи честоти. Само честотите над fs/4 с амплитуда на върха равна на 1, например, ще съдържат колебания, които са по-големи от 1.

Преобразуването x(k) → (a₁(j) | b₁(j)) е преобразуването с вълнички на Хаар от ниво 1. За да изчислим преобразуването с вълнички на Хаар от ниво 2, ще вземем преобразуването с вълнички на Хаар от ниво 1 от сигнала a₁(j).

• Ако сигнала x(k) е с дължина K, тогава сигнала a₁ е с дължина K/2 и сигнала a₂ е с дължина K/4.
• Енергията на a₁ е запазена в a₂ и b₂.
• a₁ може да бъде възстановен от сигнала a₂ и b₂ както по-горе. Тогава x(k) може да бъде възстановен от a₂, b₂ и b₁. Преобразуването с вълнички на Хаар от ниво 2 може да бъде обозначено с x → (a₂ | b₂ | b₁).

Следното е графиката на примерния сигнал a₂, който компресира оригиналния сигнал още повече.

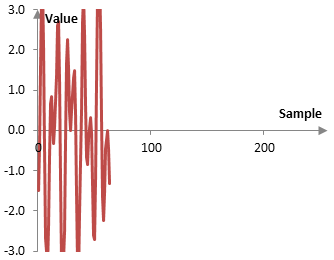
Тъй като нашият примерен сигнал е от 256 точки, този процес може да продължи до ниво 8. При ниво 8, a₈ и b₈ ще се състоят от по една единствена точка. Сигналът ще бъде компресиран до една точка.

Определение на преобразуването с вълнички на Хаар

Ако сигналът x(k) е с дължина K = 2^N за едно естествено число N, преобразуването с вълнички на Хаар от ниво на x(k) е (a_N | b_N | b_N-1 | … | b₁), където

$$a_1(j)=\frac{x(k-1)+x(k)}{\sqrt{2}}$$ $$b_1(j)=\frac{x(k-1)-x(k)}{\sqrt{2}}$$

за j = 0, 1, …, K/2 и k = 2j + 1, and

$$a_n(i)=\frac{a_{n-1}(j-1)+a_{n-1}(j)}{\sqrt{2}}$$ $$b_n(i)=\frac{a_{n-1}(j-1)-a_{n-1}(j)}{\sqrt{2}}$$

за n = 2, 3, …, N; i = 0, 1, …, K / 2ⁿ; и j = 2i + 1.

Отбелязваме, както преди, че

$$x(k-1)=\frac{a_1(j)+b_1(j)}{\sqrt{2}}$$ $$x(k)=\frac{a_1(j)-b_1(j)}{\sqrt{2}}$$ $$a_{n-1}(j-1)=\frac{a_n(i)+b_n(i)}{\sqrt{2}}$$ $$a_{n-1}(j)=\frac{a_n(j)-b_n(j)}{\sqrt{2}}$$

Вълнички на Хаар

Един друг начин, по който можем да получим един подобен резултат, е да изчислим произведението на сигнала x(k) с множеството от функции описани по-долу. За да изчислим a_N в определението по-горе, която се състои от едно единствено число, изчисли сумата на произведението на x(k) с

$$\psi^a_N (k)=\frac{1}{2^{\frac{N-1}{2}}}$$

Използваме индекса "a" за да покажем, че тази функция се използва за да се изчисли частта "a" на преобразуването с вълнички на Хаар. Използвай следните две функции за да изчислиш a_N-1, която се състои от две числа.

$$\psi^a_{N-1} (k)=\begin{cases} (-1)^m \frac{1}{2^{\frac{N-1}{2}}}, m \frac{K}{2} \le k \lt (m+1) \frac{K}{2} \\ 0, k \lt m \frac{K}{2}, k \ge (m+1) \frac{K}{2} \end{cases}, m=0,1$$

По общо, a_N-n за нивото N – n на преобразуването може да се изчисли с 2ⁿ на брой функции (n=0, 1, …, N)

$$\psi^a_{N-n} (k)=\begin{cases} (-1)^m \frac{1}{2^{\frac{N-(n+1)}{2}}}, m \frac{K}{2^n} \le k \lt (m+1) \frac{K}{2^n} \\ 0, k \lt m \frac{K}{2^n}, k \ge (m+1) \frac{K}{2^n} \end{cases}, m= 0,1,...,2^n-1$$

За да разбереш това, обърни внимание на следните графики на ψ^a₈, ψ^a₇ и ψ^a₆ от примера по-горе

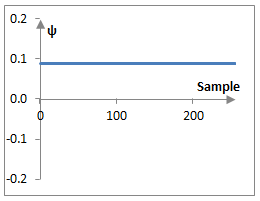
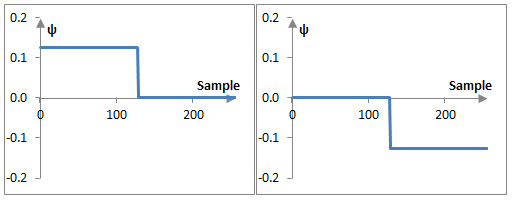
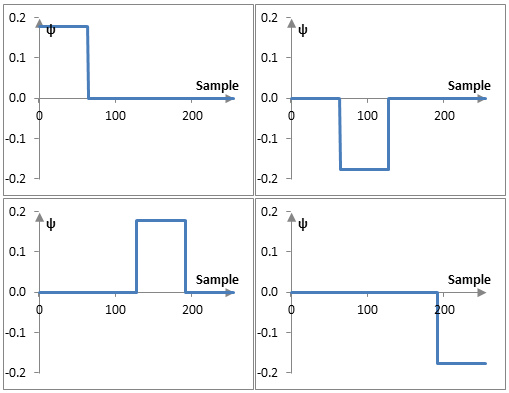
Само малко по-трудно е да се определят функциите, които могат да се използват за да се изчислят стойностите на b. Например

$$\psi^b_{1} (k)=\begin{cases} (-1)^k \frac{1}{2^{\frac{1}{2}}}, m \frac{K}{2^{N-1}} \le k \lt (m+1) \frac{K}{2^{N-1}} \\ 0, k \lt m \frac{K}{2^{N-1}}, k \ge (m+1) \frac{K}{2^{N-1}} \end{cases}, m= 0,1,...,2^{N-1}-1$$ $$\psi^b_{2} (k)=\begin{cases} (-1)^{int(\frac{k}{2})} \frac{1}{2^{\frac{2}{2}}}, m \frac{K}{2^{N-2}} \le k \lt (m+1) \frac{K}{2^{N-2}} \\ 0, k \lt m \frac{K}{2^{N-2}}, k \ge (m+1) \frac{K}{2^{N-2}} \end{cases}, m= 0,1,...,2^{N-2}-1$$ $$...$$ $$\psi^b_{n} (k)=\begin{cases} (-1)^{int(\frac{k}{2^{n-1}})} \frac{1}{2^{\frac{n}{2}}}, m \frac{K}{2^{N-n}} \le k \lt (m+1) \frac{K}{2^{N-n}} \\ 0, k \lt m \frac{K}{2^{N-n}}, k \ge (m+1) \frac{K}{2^{N-n}} \end{cases}, m= 0,1,...,2^{N-n}-1$$

n = 1, 2, …, N. Смени n и N-n в последната формула за да получиш един резултат, който прилича на определението на ψ^a. Графиките на ψ^b са доста подобни на графиките на ψ^a.

Тези видове функции често се определят (по-общо и в недискретизираното време) с

$$\psi(x)=\begin{cases} 1, 0 \le x \lt \frac{1}{2} \\ -1, \frac{1}{2} \lt x \le 1 \\ 0, x=\frac{1}{2}, x \lt 0, x \gt 1 \end{cases}$$ $$\psi_{n,m}=\psi(2^n x - m)$$

за целите числа n = 0,1, … и m=0, 1, …, 2ⁿ-1. Това са вълничките на Хаар. ψ(x) се нарича вълничката майка. Избирането на стойността ψ(0.5) = 0 има недостатъци, но това е извън обхвата на тази тема.

Тези функции са ортогонални, защото

$$\int_0^1 \psi(x) \, \psi_{n,m}(x) \, dx=0, \, (n,m) \ne (0,0)$$ $$\int_0^1 \psi_{i,j}(x) \, \psi_{n,m}(x) \, dx=0, \, (n,m) \ne (i,j)$$

Тези функции ще станат и ортонормални, ако вместо горното определение използваме

$$\psi_{n,m}=2^n \, \psi(2^n\,x-m)$$

Това определение се среща често, но с него не става веднага ясно как вълничките на Хаар могат да се използват в преобразуването с вълничките на Хаар.

Използване на преобразуването с вълничките на Хаар: компресиране на данните и намаляване на шума

Фактът, че много от стойностите, изчисление с преобразуването с вълничките на Хаар, са малки, означава, че преобразуването може да се използва за да се намали размерът на данните, които се използват.

По-точно, в примера по-горе 256 стойности съдържат преобразуването с вълнички на Хаар на сигнала: 128 стойности на b₁, 64 стойности на b₂, …, 2 стойности на b₇, една стойност на b₈ и една стойност на a₈. За да получим 2:1 компресиране, можем просто да махнем 128-те най-малки стойности и да приемем, че са нула (т.e., ще ги приравним на нула и ще пуснем сигнал само с останалите стойности – тези, които не са нула). Ако използваме тези данни, ще имаме сигнал само от 128 стойности вместо 256, плюс няколко байта, които показват какви са позициите на ненулевите стойности в оригиналния сигнал (можем например да използваме 32 байта или 8 четири байтови цели числа за да покажем дали всяка от 256-те стойности е нула или не).

Ако възстановим самият сигнал от компресираното преобразуване с вълнички на Хаар, ще получим следното.

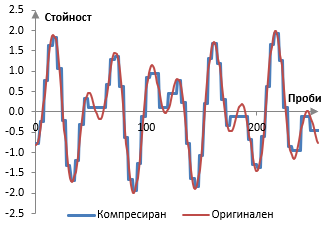
Разбира се, едно компресиране само от 2:1 не е толкова интересно и можем да получим подобно отношение с методи на компресиране, които не губят информация. Можем обаче да получим и по-добри отношения на компресиране, ако приемем малко по-голяма загуба на информация. Можем също така да получим и по-високи отношения на компресиране с вълнички, които са по-мощни от вълничките на Хаар. Същият метод може да се използва и за да се премахне случаен шум с ниско ниво от сигнала.