При работата със сигнали, амплитуден спектър на едно аналогово или цифрово оборудване или софтуер е някакво представяне, обикновено числово, графично или математическо, на това, как това оборудване или софтуер променя амплитудата на честотите. Най-често, амплитудният спектър е отношението на амплитудата на всяка честотите в изходния сигнал към амплитудата на тези честоти във входния сигнал.
Обикновено, ако искаме да опишем как една система влияе на амплитудите на честотите в сигнала, използваме термина амплитуден спектър. Ако искаме да опишем как системата променя фазите на честотите в сигнала, използваме термина фазов спектър. Ако искаме да опишем промените и в амплитудите, и в фазите на честотите в сигнала, използваме термина честотен спектър.
Пример: Амплитуден спектър на един идеален нискочестотен филтър на 8 KHz
Би трябвало да очакваме, че един идеален нискочестотен филтър ще остави ниските честоти непроменени (ще ги "пусне") и че доста ще понижи амплитудите на високите честоти (ще ги "спре"). Един идеален нискочестотен филтър тогава би трябвало да има амплитудния спектър, който е показан на следната графика.
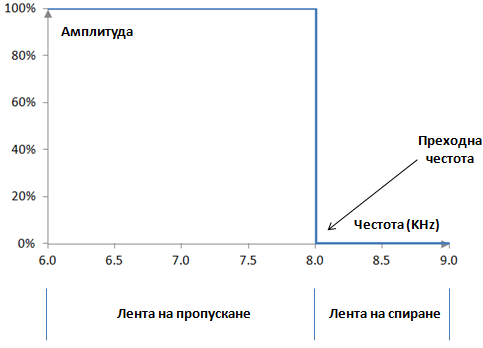
"Амплитудата" в графиката по-горе е отношението между амплитудата на изходния сигнал и амплитудата на входния сигнал за една и съща честота. 100% означава, че филтърът не променя амплитудата за определената честота. 0% означава, че филтърът в действителност премахва определената честота. Този филтър тогава оставя амплитудите на честотите под някаква "преходна" честота (8 KHz в този филтър) непроменени, а в същото време премахва (филтрира или пък спира) честотите, които са над преходната честота. Честотите, които са непроменени, се наричат "лентата / ивицата на пропускане" на филтъра. Честотите, които са премахнати, са "лентата / ивицата на спиране" на филтъра.
В математиката, амплитудният спектър H на идеалния нискочестотен филтър е функция на входната честота f и е нещо като следната.
$$|H(f)|=\begin{cases} 100\%, f \le преходна\,честота \\ 0\%, f \gt преходна\,честота \end{cases}$$
Различните филтри имат различни амплитудни спектри. Един високочестотен филтър например би трябвало да пропусне високите честоти и да спре ниските честоти. Има филтри, които пропускат само честотите в някакъв честотен интервал и спират всичко, което е под или над този интервал (средночестотни). Един филтър бразда пропуска всички честоти, освен тези в един много тесен честотен диапазон и така нататък. Един всичкопропускащ филтър би трябвало да остави амплитудите на всички честоти непроменени (но да промени тяхната фаза, т.е., има някакъв определен фазов спектър).
Пример:Амплитуден спектър на един реалистичен цифров нискочестотен филтър
Следната графика показва типичния амплитуден спектър на един цифров нискочестотен филтър.
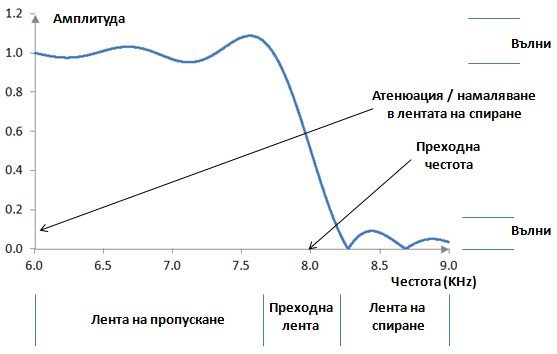
Амплитудата в тази графика е просто отношението на изходната амплитуда към входната амплитуда за определена честота. Не е показана като процент, понеже процентите обикновено не са единиците, които се използват. В повечето случаи, можете да предположите, че една такава графика входната амплитуда е 1 (т.е., тя е нормализирана или нормирана) и така изходната амплитуда е тази, която е показана на графиката.
Този нискочестотен филтър не е идеален и неговият амплитуден спектър се различава от амплитудния спектър на идеалния нискочестотен филтър. Пак има лента на пропускане – интервал от честоти, които филтърът пуска – и лента на спиране – интервал от честоти, които филтърът спира. Обикновено има обаче и преходна лента, тъй като филтъра не преминава от лентата на пропускане към лентата на спиране изведнъж, а плавно в един интервал от честоти около преходната честота. Не всички честоти, които филтърът пуска, са еднакви, понеже имат различна изходна амплитуда, която се явява като "вълни" в лентата на пропускане. Цифровите филтри имат такива характерни вълни, които са по-големи близо до преходната лента. Има и подобни вълни в лентата на спиране, които също са по-големи близо до преходната лента. Честотите в лентата на спиране не са напълно спрени и затова филтъра има "атенюация в лентата на спиране": величината, с която амплитудите на честотите в лентата на спиране са намалени.
Вълните в лентата на пропускане и в лентата на спиране са характерни за доста филтри, но не за всички филтри. Филтърът на Батъруърт например няма вълни. Амплитудният спектър на един нискочестотен филтър на Батъуърт намалява монотонно. От друга страна пък, всички филтри с ограничени импулсни спектри имат вълни, които са резултат от феномена на Гибс – израз на факта, че редовете на Фурие, които се използват за да се създадат тези филтри, са редове от непрекъснати функции, а идеалният амплитуден спектър по-горе е една функция с точка на прекъсване (въпреки че има производни, които са непрекъснати).
Същият амплитуден спектър по-горе може да бъде показан в децибели, понеже децибелите просто измерват отношението на две величини. Тук децибелът е единица за измерение на съотношението на изходните и входните амплитуди. Следното е амплитудния спектър на същия филтър, но в децибели.
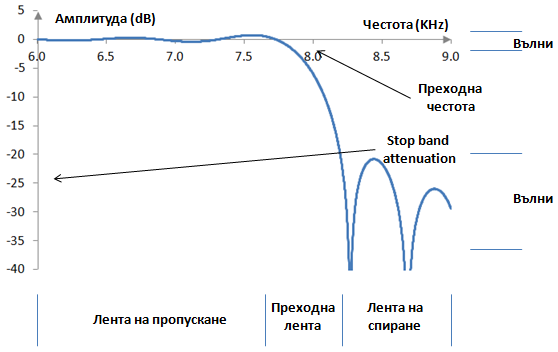
Пример: Амплитудният спектър и трансферните функции
Ако трансферната функция] , изчислена с [[z-transform, на една линейна система, която е инвариантна във времето, е H(z), амплитудният спектър на системата се дава от
$$|H(e^{j \omega})|=\sqrt{(Re(H(e^{j \omega})))^2+(Im(H(e^{j \omega})))^2}$$
където Re(H) и Im(H) са реалната и имагинерната част на комплексното число H. (Същата формула в непрекъснато време би била |H(jω)|; виж Честотен спектър за още подробности). Да кажем, че това е един цифров филтър с ограничен импулсен спектър и с дължина N, коефициенти a(k) и трансферна функция H(ejω). Можем да изчислим амплитудния спектър на този филтър според следната формула.
$$|H(f)|=\sqrt{(\sum_{k=0}^{N-1} a(k) \, \cos(\frac{2\pi k f}{f_s}))^2+(\sum_{k=0}^{N-1} a(k) \, \sin(\frac{2\pi k f}{f_s}))^2}$$
Тук H(f) е амплитудния спектър като функция на честотата f, a(k) са коефициентите на филтъра при пробите k = 0,…, N-1, а fs е честотната резолюция (пробната честота). (Заместването z = ejω в преобразуването Z произвежда преобразуването на Фурие в дискретизирано време. Формулата на Ойлер ни дава ejω = cos(ω) + j sin(ω). Ъгловата честота ω може да бъде заменена с ω = 2 π f / fs).
Добави нов коментар