The rectangular window of length N, defined for k = 0, 1, …, N – 1 is given by the formula
$$a(k)=1$$
The window has no effect when applied to a filter or a signal. It is, however, a benchmark window, against which other windows are often compared. For example, a standard low pass filter with finite impulse response will have the shortest transition band with the rectangular window.
The following is a graph of the rectangular window (N = 100).
Measures for the rectangular window
The following is a discrete Fourier transform of 500 points of the rectangular window.
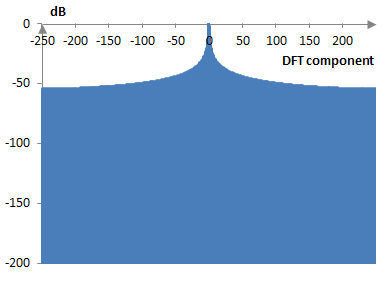
The window measures are as follows.
| Coherent gain | 1.0 |
| Equivalent noise bandwidth | 1.0 |
| Processing gain | 0.0 dB |
| Scalloping loss | -3.92 dB |
| Worst case processing loss | -3.92 dB |
| Highest sidelobe level | -13.3 dB |
| Sidelobe falloff | -6.0 dB / octave, -20 dB / decade |
| Main lobe is -3 dB | 0.88 bins |
| Main lobe is -6 dB | 1.20 bins |
| Overlap correlation at 50% overlap | 0.500 bins |
| Amplitude flatness at 50% overlap | 1.000 bins |
| Overlap correlation at 75% overlap | 0.752 bins |
| Amplitude flatness at 75% overlap | 1.000 bins |
See also:
Window
Comments
I have a question
Are you accepting advertising on your site?
Not more than what we have
Add new comment